← Joel Strait

NanoSynth

So you’ve learned the basics of how digital audio works and it’s gone to your head. Your friends can’t stand you anymore. Your parents “forget” to tell you they’ve moved. The next step toward total alienation is to flex your knowledge further by writing a program to create some simple sounds.

Good thing I’m here to help! This article describes a command-line Ruby program called NanoSynth. It can create 5 different simple sounds, played at different notes and volumes. It shows the basics of how to write a program that creates sound.

Go ahead and check out the code on GitHub. The rest of this article goes into detail about how it works.

The Cast

NanoSynth can create 5 different types of sound wave: sine, square, sawtooth, triangle, and white noise. These wave forms look and sound like this:

Sine

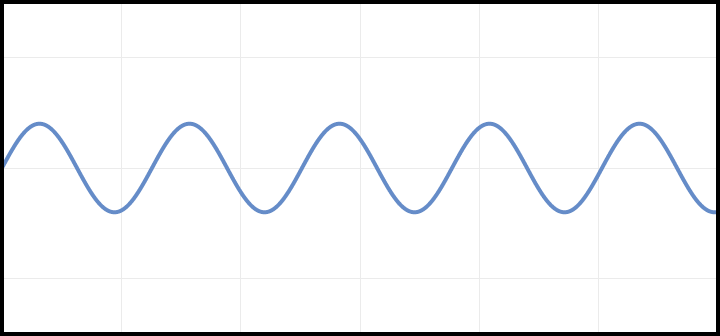
Square

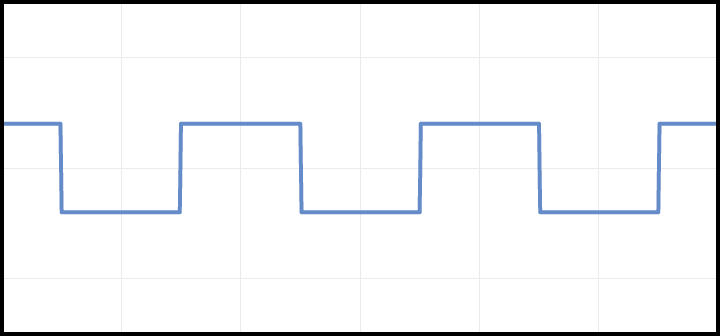
Sawtooth

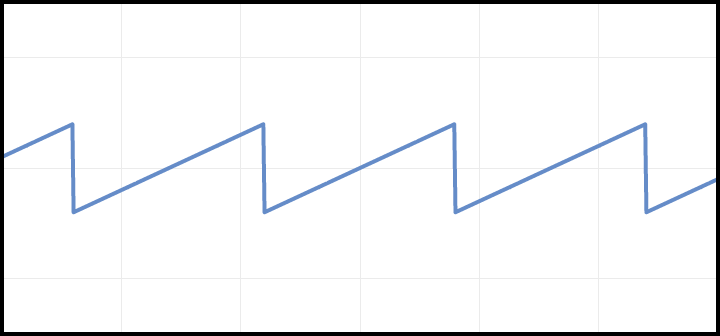
Triangle

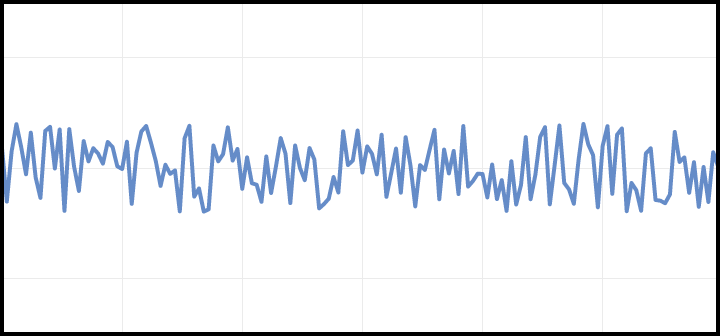
White Noise

By themselves, they sound like something you would hear out of an 8-bit Nintendo console. However, analog synthesizers use these types of waves as the building blocks for more complex sounds.

Basic Outline

When you run NanoSynth, you specify the wave type, frequency, and maximum amplitude (i.e. volume). NanoSynth then generates 1 second worth of sample data. This data is then written to a Wave file on disk using the WaveFile gem. To hear the sound, you can play the Wave file in whatever media player you like.

NanoSynth can be thought of as two main parts: the part that reads the command-line arguments, writes the generated sample data to a Wave file (using the WaveFile gem) and generally drives things, and the part that actually generates the audio data. Let’s get the first part out of the way, so we have a shell to fill out. Here it is:

gem "wavefile", "=1.1.1"
require "wavefile"

OUTPUT_FILENAME = "mysound.wav"
SAMPLE_RATE = 44100
SECONDS_TO_GENERATE = 1
TWO_PI = 2 * Math::PI
RANDOM_GENERATOR = Random.new

def main
  # Read the command-line arguments.
  waveform = ARGV[0].to_sym  # Should be "sine", "square", "saw", "triangle", or "noise"
  frequency = ARGV[1].to_f   # 440.0 is the same as middle-A on a piano.
  amplitude = ARGV[2].to_f   # Should be between 0.0 (silence) and 1.0 (full volume).
                             # Amplitudes above 1.0 will result in clipping distortion.

  # Generate sample data at the given frequency and amplitude.
  # The sample rate indicates how many samples we need to generate for
  # 1 second of sound.
  num_samples = SAMPLE_RATE * SECONDS_TO_GENERATE
  samples = generate_sample_data(waveform, num_samples, frequency, amplitude)

  # Wrap the array of samples in a Buffer, so that it can be written to a Wave file
  # by the WaveFile gem. Since we generated samples with values between -1.0 and 1.0,
  # the sample format should be :float
  buffer = WaveFile::Buffer.new(samples, WaveFile::Format.new(:mono, :float, SAMPLE_RATE))

  # Write the Buffer containing our samples to a monophonic Wave file
  WaveFile::Writer.new(OUTPUT_FILENAME, WaveFile::Format.new(:mono, :pcm_16, SAMPLE_RATE)) do |writer|
    writer.write(buffer)
  end
end

# The dark heart of NanoSynth, the part that actually generates the audio data
def generate_sample_data(wave_type, num_samples, frequency, max_amplitude)
  # We're gonna fill this in, but for now just return an empty list of samples.
  return []
end

main

This is intentially minimal, to keep things focused on the actual sound generating portion. For example, the command-line arguments aren’t validated - if you give bad arguments when running NanoSynth, it will crash or not work right.

Save this to a file called nanosynth.rb.

Next, install the WaveFile gem. If you’re using rbenv or RVM, you can install it like this:

gem install wavefile --version 1.1.1

If you’re using the built-in Ruby that comes with a Mac, you might need to use sudo when installing the gem:

sudo gem install wavefile --version 1.1.1

Finally, from the command line navigate to the folder containing nanosynth.rb. Run it like this:

ruby nanosynth.rb sine 440.0 0.2

This should create a file called mysound.wav in the current folder, containing a sine wave at 440Hz and 20% full volume. If you try to play it though, you won’t hear anything. That’s because we haven’t filled in the generate_sample_data() method yet. When we’re done though, it will!

Generating Sample Data

Next we need to implement the generate_sample_data() method. If you’ve read the digital audio primer, you’ll know we need a method that will generate an array of samples between -1.0 and 1.0. Since NanoSynth uses a sample rate of 44,100Hz and generates 1 second of sound, the array should contain 44,100 values.

Our method will be able to generate sine, square, sawtooth and triangle waves, as well as white noise. It will also allow passing in a frequency to determine the pitch of the generated tone, as well as the amplitude to determine the loudness.

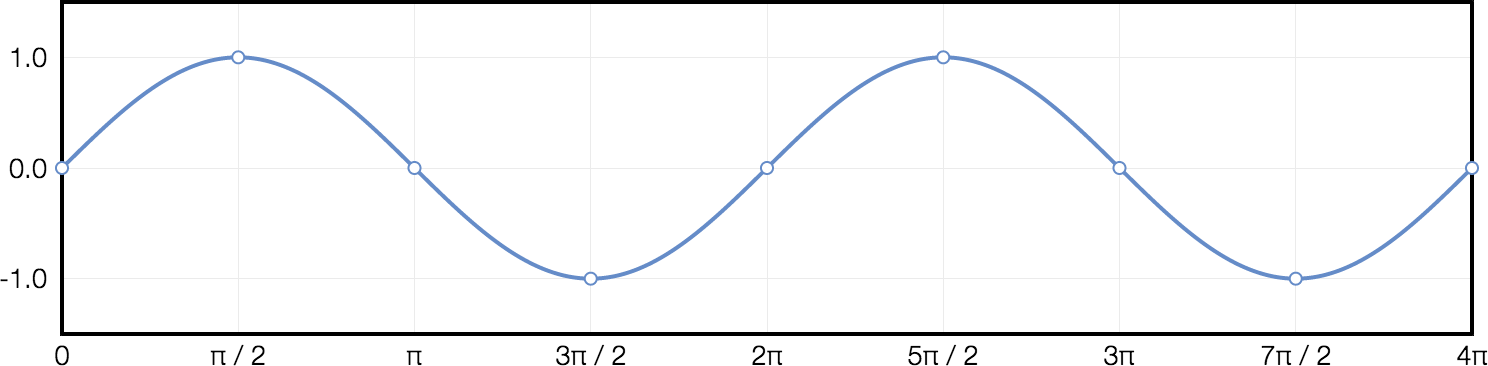
Sine Waves

Let’s start with sine waves. They hold a hallowed position as the fundamental building block of sound. In fact, any possible sound (including the other waveforms in this article) can be re-created by combining the correct sine waves together. (Thanks to @fourier for figuring this out).

A sine wave looks like this:

You can generate values in a sine wave by using Ruby’s built-in Math::sin() function. It takes an x-value in radians, and returns the height of the sine wave at that x-value.

Math::sin(0.0)             # Returns 0.0
Math::sin(Math::PI * 0.5)  # Returns 1.0
Math::sin(Math::PI)        # Returns 0.0
Math::sin(Math::PI * 1.5)  # Returns -1.0
Math::sin(Math::PI * 2)    # Returns 0.0

An important fact about the sine wave is that it has a period of 2π radians (about 6.28). If you call Math::sin() with values from 0.0 to ~6.28, you’ll see the y-value returned go from 0.0 up to 1.0, down to -1.0, then back up to 0.0 when you get to ~6.28. If you then keep incrementing the x-value you’ll see the values repeat again, with another full cycle ending at ~12.57 (4π).

So let’s say we want to generate a sine wave with a frequency of 1Hz. Assuming we’re using the common sample rate of 44,100Hz (i.e. 44,100 samples every second), we could do it like this:

position_in_period = 0.0                   # Range of 0.0 to 1.0
position_in_period_delta = 1.0 / 44100.0   # Frequency divided by sample rate

# Initialize an array of samples set to 0.0. Each sample will be replaced with
# an actual value below.
samples = [].fill(0.0, 0, num_samples)

num_samples.times do |i|
  samples[i] = Math::sin(position_in_period * TWO_PI) * max_amplitude

  position_in_period += position_in_period_delta

  # Constrain the position in period between 0.0 and 1.0
  # I.e., re-loop over the same cycle again and again
  if position_in_period >= 1.0
    position_in_period -= 1.0
  end
end

Think of it like this. We start at 0, and the finish line for one cycle is 2π (~6.28). Each time through the loop, we increment position_in_period, getting closer to the finish line of 2π. Once we go past the finish line, we’ll loop back around to the start of the cycle and keep going.

The code above will give us a nice 1Hz sine wave, but unfortunately humans can’t hear anything below about 20Hz. If you save it to a wave file and play it back, you won’t hear anything! No problem though, when calculating position_in_period_delta, we can plug in a higher frequency to get something we actually can hear. Let’s try 440Hz, which is the same as middle A on a piano.

position_in_period_delta =   1.0 / 44100.0  # i.e. 0.000023
position_in_period_delta = 440.0 / 44100.0  # i.e. 0.009977

Notice how 440Hz makes position_in_period_delta larger. This means each time through the loop we’ll get to 2π faster, and therefore complete one cycle faster. So to change the frequency of a sine wave, all you need to is plug in a different frequency when calculating position_in_period_delta.

The sine function returns values between -1.0 and 1.0. By convention these also happen to be the equivalent to the minimum and maximum amplitudes our speakers can play, so this means a generated sine wave will play at full volume. If we want to make it quieter, we can multiply each sample by a constant amount. For example to have it play at half of maximum volume, multiply everything by 0.5. If you multiply each sample by a number greater than 1.0, you’ll cause clipping to occur, which is a type of distortion. Unless you’re purposely trying to cause distortion or weird sound effects you don’t want to do that. (This applies to any waveform, not just the sine wave).

Let’s add this final code to our template:

def generate_sample_data(wave_type, num_samples, frequency, max_amplitude)
  position_in_period = 0.0
  position_in_period_delta = frequency / SAMPLE_RATE

  # Initialize an array of samples set to 0.0. Each sample will be replaced with
  # an actual value below.
  samples = [].fill(0.0, 0, num_samples)

  num_samples.times do |i|
    # Add next sample to sample list. The sample value is determined by
    # plugging the period offset into the appropriate wave function.

    if wave_type == :sine
      samples[i] = Math::sin(position_in_period * TWO_PI) * max_amplitude
    end

    position_in_period += position_in_period_delta

    # Constrain the period between 0.0 and 1.0
    if position_in_period >= 1.0
      position_in_period -= 1.0
    end
  end

  samples
end

Next, run NanoSynth, using a frequency of 440Hz, and an amplitude of 20% full volume:

ruby nanosynth.rb sine 440.0 0.2

This should write mysound.wav to the current directory, and it should sound like this:

Square Waves

Next up, let’s create a square wave. In a certain sense square waves are simpler than sine waves, because they consist of switching back and forth between just two different amplitudes. For example a certain number of samples at amplitude -0.75, followed by an equal number of samples at amplitude 0.75, and then repeated. Square waves have an especially 8-bit Nintendo sound to them. They are also important in subtractive synthesis, since they contain harmonics, while sine waves don’t. However, that’s beyond the scope of this article.

The amplitude for a square wave determines the two amplitudes it switches between. For example, for an amplitude of 0.75, a square wave will toggle between 0.75 and -0.75. The rate at which the two amplitudes are toggled determines the frequency. The faster the toggle, the higher the frequency (and thus the higher the pitch).

A square wave looks like this:

Here are some more concrete examples:

To generate a square wave, we can take the position_in_period variable we already have, which ranges from 0.0 to 1.0. If it’s less that 0.5 use the positive amplitude, and if it’s greater-or-equal to 0.5, use the negative amplitude.

With that in mind, here’s the updated generate_sample_data() method so that it generates a square wave for us. This code is the same as before, except for the changes highlighted in yellow.

def generate_sample_data(wave_type, num_samples, frequency, max_amplitude)
  position_in_period = 0.0
  position_in_period_delta = frequency / SAMPLE_RATE

  # Initialize an array of samples set to 0.0. Each sample will be replaced
  # with an actual value below.
  samples = [].fill(0.0, 0, num_samples)

  num_samples.times do |i|
    # Add next sample to sample list. The sample value is determined by
    # plugging the period offset into the appropriate wave function.

    if wave_type == :sine
      samples[i] = Math::sin(position_in_period * TWO_PI) * max_amplitude
    elsif wave_type == :square
      samples[i] = (position_in_period >= 0.5) ? max_amplitude : -max_amplitude
    end

    position_in_period += position_in_period_delta

    # Constrain the period between 0.0 and 1.0
    if position_in_period >= 1.0
      position_in_period -= 1.0
    end
  end

  samples
end

After adding this code go to the command line, and run:

ruby nanosynth.rb square 440.0 0.2

Open mysound.wav in your favorite media player. It should sound like this:

Sawtooth Waves

Sawtooth waves are named for their appearance, because their waveform looks like the edge of a saw. Along with square and triangle waves, they are used in subtractive synthesis.

The waveform for each period consists of a straight line ramp going from a sample with the minimum amplitude to a sample with the maximum amplitude (or vice versa). When the next period begins, the waveform jumps back up to the starting point and repeats.

To generate this, we need to calculate continuously increasing (or decreasing) numbers. We already have position_in_period which ranges from 0.0 to 1.0, so we can scale it to range between -1.0 and 1.0 instead.

That is, we can:

The rest of our existing code that increments position_in_period will do the rest.

if wave_type == :sine
  samples[i] = Math::sin(position_in_period * TWO_PI) * max_amplitude
elsif wave_type == :square
  samples[i] = (position_in_period >= 0.5) ? max_amplitude : -max_amplitude
elsif wave_type == :saw
  samples[i] = ((position_in_period * 2.0) - 1.0) * max_amplitude
end

To test this out, run:

ruby nanosynth.rb saw 440.0 0.2

It should sound like this:

Triangle Waves

Triangle waves sound like a cross between a sine wave and a square wave. It resembles a sine wave made out of straight lines rather than an S curve.

One way to generate a triangle wave is to start with a saw wave. Notice how half of the samples in a saw wave will be below 0, and half will be above. If you take the absolute value of each sample, you’ll get a triangle pattern.

This is close to what we need, but it’s not scaled properly. For example, if our amplitude is 0.5, we want the samples in our triangle wave to span from -0.5 to 0.5. However, just taking the absolute value of a saw wave will give us samples that range from 0.0 to 0.5. No problem - we can multiple the samples in our proto-triangle wave by 2, and then subtract them from our amplitude.

if wave_type == :sine
  samples[i] = Math::sin(position_in_period * TWO_PI) * max_amplitude
elsif wave_type == :square
  samples[i] = (position_in_period >= 0.5) ? max_amplitude : -max_amplitude
elsif wave_type == :saw
  samples[i] = ((position_in_period * 2.0) - 1.0) * max_amplitude
elsif wave_type == :triangle
  samples[i] = max_amplitude - (((position_in_period * 2.0) - 1.0) * max_amplitude * 2.0).abs
end

To test this out, run:

ruby nanosynth.rb triangle 440.0 0.2

It should sound like this:

White Noise

White noise is random samples. It sounds like radio static. It can be useful for making snare drum sounds if you apply an envelope to it (beyond the scope of this article).

To generate white noise we need to generate random numbers between the maximum and minimum amplitudes. We can use Ruby’s built-in Random class to do this - the rand method lets you pass in a range that the random number should be within.

if wave_type == :sine
  samples[i] = Math::sin(position_in_period * TWO_PI) * max_amplitude
elsif wave_type == :square
  samples[i] = (position_in_period >= 0.5) ? max_amplitude : -max_amplitude
elsif wave_type == :saw
  samples[i] = ((position_in_period * 2.0) - 1.0) * max_amplitude
elsif wave_type == :triangle
  samples[i] = max_amplitude - (((position_in_period * 2.0) - 1.0) * max_amplitude * 2.0).abs
elsif wave_type == :noise
  samples[i] = RANDOM_GENERATOR.rand(-max_amplitude..max_amplitude)
end

To test this out, run:

ruby nanosynth.rb noise 440.0 0.2

Note that the frequency argument doesn’t matter for white noise - since these are random samples, the frequency won’t affect the output. It should sound something like this:

Some Things You Can Try Next

Also at GitHub Copyright © 2005—23 Joel Strait